Home
必勝法検証
バーネット法(1326法)の検証

バーネット法(1326法)の検証

シミュレーターで検証（バーネット法）

■バーネット法(1326法)とは

バーネット法（Barrett Method）、別名「1326法」とは、ギャンブルにおけるベッティングシステムの一つです。バカラやルーレットの赤黒等、的中確立が約1/2程度なら儲かる仕組みになっています。

このシステムは他の有名なシステム（例えばココモ法やマーチンゲール法）ほど一般的ではなく、あまり知られていません。そのため、特定のルールや詳細な解説が公式に確立されているわけではないことが特徴です。

1、3、2、6とベットしていく戦略

■賭け方

配当が2倍以上のゲームで、当たり続けてる限り以下のルールでベットします。
1ゲーム目：1ベット、2ゲーム目：3ベット、3ゲーム目：2ベット、4ゲーム目以降：6ベットします。
1、3、2、6、6、6...です。（※6で当たったら1に戻るというやり方もあるようです）
ハズレで終了し、また1からに戻ります。

【バーネット法(1326法)早見表】※配当は2倍とする

回数	ベット額	勝敗	配当	利益
1	1	×	0	-1
2	1	〇	2	0
3	3	〇	6	3
4	2	〇	4	5
5	6	〇	12	11
6	6	〇	12	17
7	6	×	0	11
8	1	×	0	10
9	1	〇	2	11
10	3	〇	6	14

■バーネット法(1326法)のシミュレーション方法

・ゲームはヨーロピアンスタイルのルーレット（0～36）とします。
　（オッズが2倍以上なら、競馬や競艇でも可）
・ハイロー(ロー：1～18、ハイ：19～36にベットする方法)でローにベットしたとします。
　配当は2倍。(1～18で勝利 ※確立約48.6％)
・ゲーム回数は1000ゲーム。1000ゲーム時点でサイクルが途中でも強制終了。
・ハズレるまでを1サイクルとします。

マーチンゲール法の検証シミュレーションルーレットハイロー

毎回結果が変わります。結果ページのF5:再表示でも可。
シミュレーター項目説明

※シミュレーション結果、または結果を利用したグラフ等をホームページに掲載される場合は、引用元の紹介とリンクを掲載をしていただけると非常に嬉しいです。

■バーネット法(1326法)の検証結果グラフ

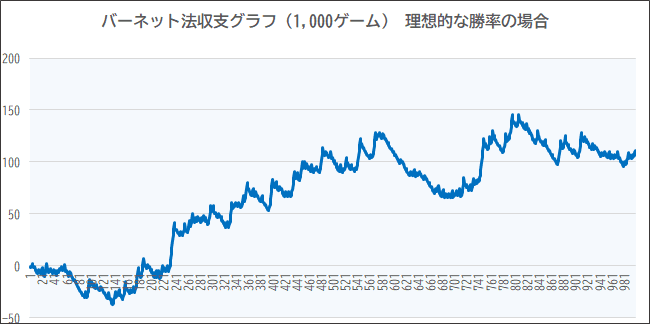
●勝利回数：512回　●サイクル内最多ゲーム数：11回（※最大連勝11、最大連敗10）
●最終収支：111　　●最小収支：-37　●最大収支：146

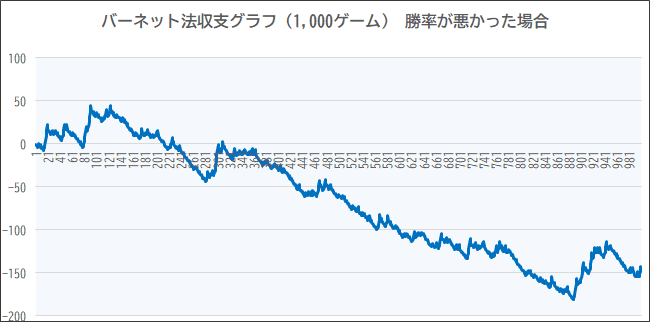
●勝利回数：465回　●サイクル内最多ゲーム数：9回（※最大連勝9、最大連敗11）
●最終収支：-143　 ●最小収支：-181　●最大収支：44

20連敗までの確率と投資額

■計算条件：ヨーロピアンルーレットのハイロー
■計算式：負ける確率をPとすると、n連敗の確率は以下

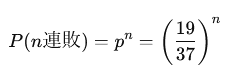
ルーレットハイロー連敗確率式

【バーネット法 20連敗早見表】

連敗数	確率(％)	ベット額	通算投資額
1	51.35	1	1
2	26.36	1	2
3	13.53	1	3
4	6.94	1	4
5	3.56	1	5
6	1.83	1	6
7	0.94	1	7
8	0.48	1	8
9	0.24	1	9
10	0.12	1	10
11	0.06	1	11
12	0.03	1	12
13	0.02	1	13
14	0.01	1	14
15	0.006	1	15
16	0.003	1	16
17	0.002	1	17
18	0.001	1	18
19	0.0006	1	19
20	0.0003	1	20